Площадь треугольника через углы, формула

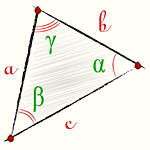
Площадь треугольника через две стороны и угол между ними, формула

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.

\[ S = \frac{1}{2} a b \sin(γ) \]

\[ S = \frac{1}{2} a c \sin(β) \]

\[ S = \frac{1}{2} b c \sin(α) \]

Площадь треугольника через одну сторону и прилежащие к ней углы, формула

Если известна одна сторона треугольника и два прилежащих к ней угла, то площадь данного треугольника вычисляется, как половина квадрата данной стороны умноженная на дробь, в числителе которой, произведение синусов прилежащих углов, а в знаменателе синус противолежащего угла. Противолежащий угол вычисляется по формуле:

\[ γ = 180° - (α + β) \]

\[ β = 180° - (α + γ) \]

\[ α = 180° - (β + γ) \]

Площадь треугольника вычисляется по формулам:

\[ S = \frac{1}{2} a^2 \frac{\sin(β)\sin(γ)}{\sin(α)} \]

\[ S = \frac{1}{2} b^2 \frac{\sin(α)\sin(γ)}{\sin(β)} \]

\[ S = \frac{1}{2} c^2 \frac{\sin(α)\sin(β)}{\sin(γ)} \]

Назад Вперед