Площадь сегмента круга, окружности, формула

Площадь сегмента круга, окружности Сегмент круга, окружности — это часть круга, окружности, ограниченная дугой и стягивающей ее хордой.

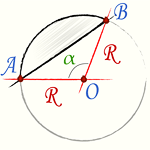
Площадь сегмента круга, окружности находится, как разность площади сектора AOB и площади равнобедренного треугольника AOB выраженную через угол

\[ S_{сегм} = S_{сект} - S_{треуг} \]

Площадь сегмента круга, окружности, если угол в градусах

\[ S_{сегм} = \frac{R^2}{2} ( \pi \frac{α°}{180°} - \sin(α°) ) \]

Вычислить, найти площадь сегмента круга, окружности, если угол в градусах

Площадь сегмента круга, окружности, если угол в радианах

\[ S_{сегм} = \frac{R^2}{2} ( α - \sin(α) ) \]

Вычислить, найти площадь сегмента круга, окружности, если угол в радианах

Назад Вперед

Copyright © FXYZ.ru, 2007 — 2024.
Мобильная β версия | полная