Высота треугольника, формула.

Высота треугольника это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение (сторона, на которую опускается перпендикуляр, в данном случае называется основанием треугольника).

В тупоугольном треугольнике две высоты падают на продолжение сторон и лежат вне треугольника. Третья внутри треугольника.

В остроугольном треугольнике все три высоты лежат внутри треугольника.

В прямоугольном треугольнике катеты служат высотами.

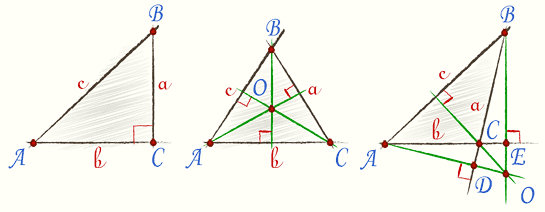
Все три высоты всегда пересекаются в одной точке, называемой Ортоцентр. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В Остроугольном - внутри треугольника. В прямоугольном треугольнике, совпадает с вершиной прямого угла.

Высота треугольника опущенная на сторону a обозначается буквой h_a и через три стороны треугольника выражается формулой:

\[ h_a = 2\frac{\sqrt{p(p-a)(p-b)(p-c)}}{a} \]

где

\[ p=\frac{1}{2}(a+b+c) \]

(a, b, c - стороны треугольника; h_a - высота треугольника)

Вычислить, найти высоту треугольника по формуле (1).

Назад Вперед