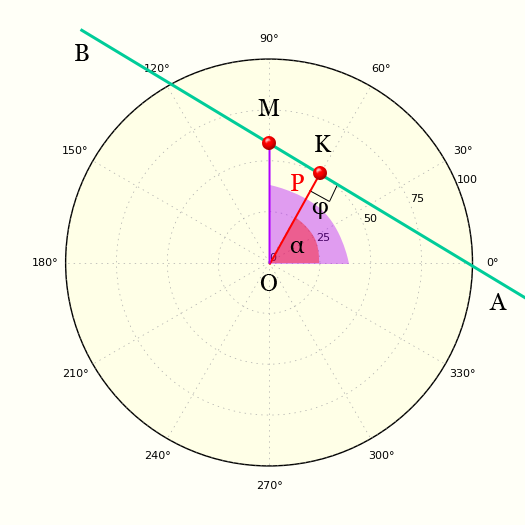
Прямая в полярных координатах

Прямая в полярных координатах вне полюса

Для получения уравнения прямой в полярных координатах рассмотрим рисунок, на котором полюс лежит вне прямой.

Прямая в полярных координатах вне полюса

Согласно этого рисунка прямую в полярных координатах можно представить следующим уравнением:

\[ ρ = \frac{P}{\cos(φ-α)} \]

Здесь

ρ, φ	полярные координаты,
P, α	Константы - полярные параметры прямой,
P	Длина нормали опущенной из полюса на прямую,
α	Угол между полярной осью и нормалью к прямой.

Это уравнение получается если рассмотреть треугольник OKM и посмотреть определение косинуса

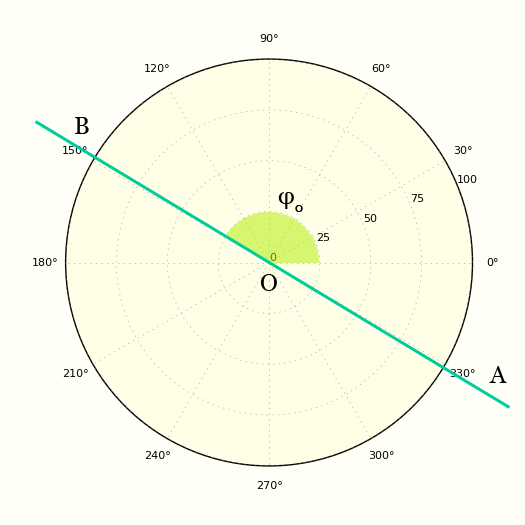
Прямая в полярных координатах проходящая через полюс

Однако когда P = 0, то прямая проходит через полюс и уравнение (1) больше не описывает прямую. Для описания прямой проходящей через полюс достаточно угла между прямой и полярной осью.

\[ φ = φ_0 \]