Угол между двумя прямыми

Пусть две неперпендикулярные прямые L1, L2 (взятые в данном порядке) представляются уравнениями

\[ \begin{cases} y = a_{1} x + b_{1} \\ y = a_{2} x + b_{2} \end{cases} \]

Тогда угол между двумя прямыми найдется по формуле

\[ \tg(θ) = \frac{a_{2} - a_{1}}{1 + a_{1} a_{2}} \]

Угол между двумя прямыми

Если прямые L1 и L2 перпендикулярны (θ = ± 90°)

то выражение стоящее в знаменателе, обращается в нуль

\[ 1 + a_{1} a_{2} = 0 \]

и частное перестает существовать. Одновременно перестает существовать («обращается в бесконечность») tg(θ). Формула (2), понимаемая буквально, теряет смысл, но в этом случае ее нужно понимать условно. Именно, всякий раз, как в знаменателе появляется нуль, угол θ надо считать равным ±90° (как поворот на +90°, так и поворот на -90° совмещает любую из перпендикулярных прямых с другой).

Если хотя бы одна из прямых L1, L2 (или обе) параллельна оси OY

то формула (2) вовсе неприменима, ибо тогда одну из прямых (или обе) нельзя представить уравнением вида (1).

В этом случае угол θ определяется следующим образом:

а) когда прямая L2 параллельная оси OY, а L1 не параллельна, применяем формулу

\[ \tg(θ) = \frac{1}{a_{1}} \]

б) когда прямая L1 параллельна оси OY, а L2 не параллельна, применяем формулу

\[ \tg(θ) = -\frac{1}{a_{1}} \]

в) когда обе прямые параллельны оси OY, они параллельны и между собой, так что

\[ \tg(θ) = 0 \]

Найти угол между двумя прямыми по формуле (2)

Угол между двумя прямыми, заданными уравнениями

\[ \begin{cases} А_{1} x + В_{1} y + С_{1} = 0 \\ А_{2} x + В_{2} y + С_{2} = 0 \end{cases} \]

можно найти по формуле

\[ \tg(θ) = \frac{A_{1} B_{2} - A_{2} B_{1}}{A_{1} A_{2} + B_{1} B_{2}} \]

При

\[ A_{1} A_{2} + B_{1} B_{2} = 0 \]

формула, понимаемая условно, дает

\[ θ = \plusmn 90° \]

Найти угол между двумя прямыми по формуле (9)

Примеры

Пример 1.

Найти угол между двумя прямыми

\[ \begin{cases} y = 2x - 3 \\ y = -3x + 2 \end{cases} \]

Здесь

\[ a_1 = 2, a_2 = -3 \]

По формуле (2) находим:

\[ \tg(θ) = \frac{-3-2}{1 + 2 \cdot (-3)} = 1 \]

Отсюда

\[ θ = \pm 45° \]

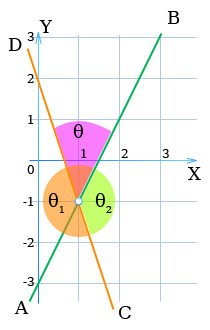
Это значит, что прямая АВ

\[ y = 2x – 3 \]

повернутая на угол +45° около точки пересечения М(1; -1) данных прямых, совместится с прямой CD

\[ y = -3x + 2 \]

Можно взять также

\[ θ = 180° + 45° = 225° \]

\[ θ = -180° + 45° = -135° \]

и т. д.

Эти углы обозначены θ₁, θ₂ на рисунке

Пример 2.

Найти угол между двумя прямыми

\[ \begin{cases} y = -3x + 2 \\ y = 2x - 3 \end{cases} \]

Прямые здесь те же, что и в примере 1, но теперь прямая CD — первая, а прямая AB — вторая. Формула (2) дает

\[ \tg(θ) = - 1 \]

т.е.

\[ θ = -45° \]

(или θ = 135°, или θ = -225° и т. д.).

На этот угол надо повернуть прямую CD до совмещения с AB.

Пример 3.

Найти угол между прямыми

\[ \begin{cases} y = 2x - 3 \\ y = -\frac{1}{2}x + 7 \end{cases} \]

\[ a_1 = 2, a_2 = -\frac{1}{2} \]

Если предварительно поставить вопрос: перпендикулярны ли эти прямые, то по признаку перпендикулярности двух прямых получим утвердительный ответ,

так что и без формулы (2) получаем

\[ θ = ± 90° \]

То же дает и формула (2). Мы получаем:

\[ \tg(θ) = \frac{-\frac{1}{2}-2}{1 + (-\frac{1}{2}) \cdot 2} = \frac{-1}{0} \]

Назад Вперед

A₁	B₁
A₂	B₂