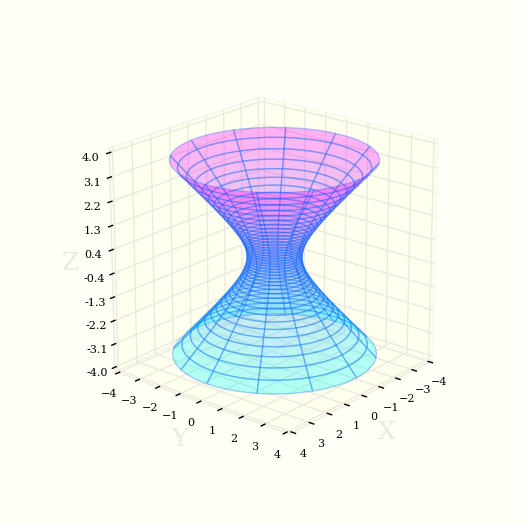
Однополостный гиперболоид, Уравнение однополостного гиперболоида

уравнение поверхности второго порядка

Однополостный гиперболоид с центром в начале координат представлен уравнением второй степени.

Наименование гиперболоид происходит от того, что среди сечений этой поверхности есть гиперболы. Эти сечения предсталяются уравнениями:

и

Название Однополостный подчеркивает, что поверхность не разорвана на две полости, а представляет собой одну сплошную бесконечную трубку, вытянутую вдоль оси OZ.

Построить поверхность однополостного гиперболоида в 3D