Эллиптический параболоид, уравнение эллиптического параболоида

уравнение поверхности второго порядка

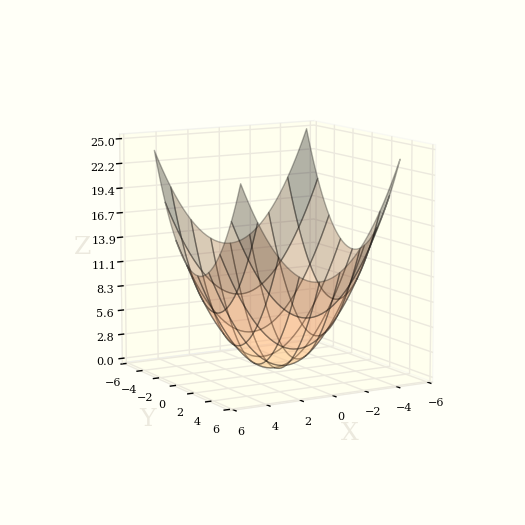
Поверхность, представляемая уравнением

\[ z = \frac{x^2}{2p} + \frac{y^2}{2q} \]

при (p > 0, q > 0), носит название эллиптический параболоид.

Сечения плоскостями XOZ и YOZ (главные сечения — это параболы).

\[ x^2 = 2pz \] \[ y^2 = 2qz \]

Обе параболы обращены вогнутостью в одну сторону (вверх).

Плоскость z=0 касается параболоида в точке O, плоскости z=h при h>0 пересекают эллиптический параболоид подобными между собой эллипсами.

\[ \frac{x^2}{2p} + \frac{y^2}{2q} = h \]

с полуосями

\[ \sqrt{2ph} \]

\[ \sqrt{2qh} \]

При h<0 эти плоскости не встречают параболоида.

Эллиптический параболоид не имеет центра симметрии. Он симметричен относительно плоскостей XOZ и YOZ и относительно оси OZ. Прямая OZ называется осью эллиптического параболоида. Точка O — его вершиной, величины p и q — параметрами.

При p = q параболы становятся равными, эллипсы обращаются в окружности и параболоид становится поверхностью порождаемой вращением параболы около ее оси (параболоид вращения).

Эллиптический параболоид можно определить как поверхность получаемую равномерным сжатием параболоида вращения к одному из его меридианов.