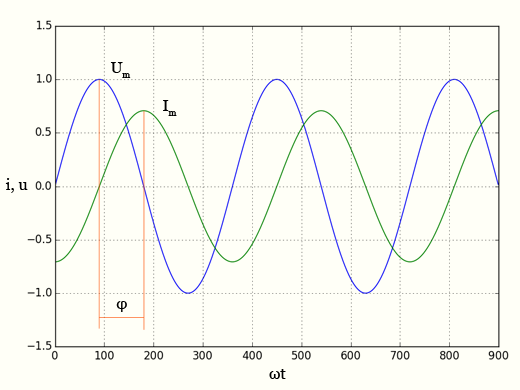
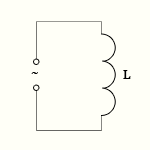
Индуктивное сопротивление

Индуктивное сопротивление

Индуктивность L в электрической цепи вызывает запаздывание тока (см Самоиндукция). Вследствие этого ток достигает максимального значения Im позже напряжения. Если R = 0, приложенное напряжение противоположно индуцированному напряжению:

\[ u = L \frac{di}{dt} = \frac{d}{dt}(LI_{m} \sin(ωt)) \]

отсюда

\[ u = ωLI_{m} \cos(ωt) \]

или

\[ u = ωLI_{m} \sin(ωt + \frac{π}{2}) \]
Индуктивное сопротивление - графики тока и напряжения
Индуктивное сопротивление — графики тока и напряжения
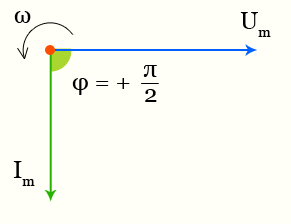
Индуктивное сопротивление - векторная диаграмма

Между напряжением и током возникает разность фаз (сдвиг фаз) равная +π/2.

B цепи переменного тока, содержащей только индуктивность, напряжение опережает ток на π/2 (или Т/4).

На векторной диаграмме ток — напряжение векторы вращаются против часовой стрелки с угловой скоростью ω. Угол между векторами напряжения и тока соответствует сдвигу фаз
\[ φ = φ_u - φ_i \]

Из написанного выше равенства следует, что амплитуда напряжения Um = ωLIm. Сопоставляя это выражение с законом Ома Um = RIm, мы видим, что величина ωL играет роль сопротивления.

Цепь переменного тока, содержащая индуктивность L, обладает сопротивлением переменному току; оно называется индуктивным сопротивлением XL.

Единица СИ индуктивного сопротивления: [XL] = Ом.

Если

XLиндуктивное сопротивление цепи переменного тока,Ом
Lиндуктивность цепи,Генри
ω = 2πfкруговая частота переменного тока,Радиан/Секунда

то имеем

\[ X_{L} = ωL \]

Индуктивное сопротивление XL растет с увеличением частоты. для постоянного тока (f = 0) оно равно нулю.

При наличии в цепи только индуктивного сопротивления сила тока определяется выражением

\[ I = \frac{U}{ωL} \]

Вычислить, найти индуктивное сопротивление

Вычислить
нажмите кнопку для расчета
Назад Вперед

Copyright © FXYZ.ru, 2007 — 2024.
Мобильная β версия | полная