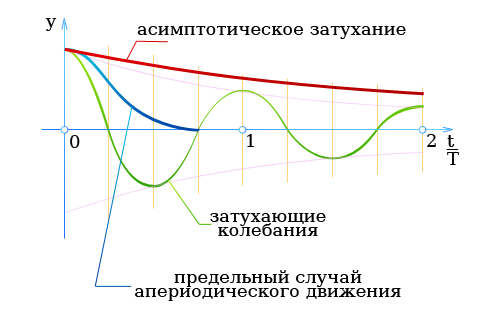
Апериодическое движение

то колебательная система после однократного возмущения асимптотически возвращается в состояние покоя (асимптотическое затухание); быстрее всего это происходит при

(предельный случай апериодического движения).

Апериодическое движение, асимптотическое затухание

m	масса системы,	кг
D	жесткость системы,	Ньютон/метр
δ	коэффициент затухания,	радиан/сек
β	коэффициент вязкого трения,	кг/сек
ω₀	собственная угловая частота,	радиан/сек

Предельный случай апериодического движения

\[ δ > ω_0 ,\qquad β > 2\sqrt{mD} ,\qquad ω – мнимая \enspace величина \]

В технике часто бывает необходимо предотвратить появление колебаний системы (например, в электрических измерительных устройствах). Для этого следует предусмотреть такое демпфирование (например, демпфирование вихревого тока), чтобы имел место предельный случай апериодического движения.

Для достижения такого демпфирования нельзя использовать внешнее (сухое) трение (например, в опорах), поскольку последнее не зависит от скорости: колебательная система будет «замирать» вблизи положения равновесия. Это имеет место у весов, пружин амортизаторов и т.д.