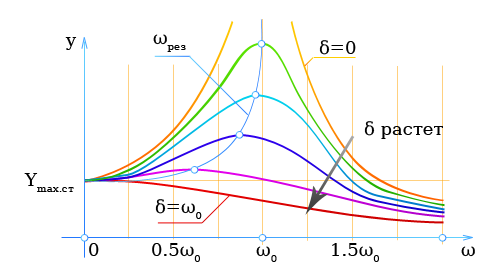
Резонанс

При заданных возмущающей силе Fmax.возм и коэффициенте трения β амплитуда Ym является функцией только угловой частоты возмущающей силы.

Резонанс

На рисунке показана зависимость Ym от ω (резонансная кривая). Параметром служит коэффициент затухания δ.

При ω ≈ ω0 она достигает особенно большого значения (резонанс).

При самых малых значениях δ величина Ym резко возрастает.

Если δ > 0, то в случае резонанса ω < ω0; величина Ymax.ст представляет собой статическое отклонение системы под действием постоянной силы Ymax.возм (ω = 0).

Для определения резонансной частоты необходимо найти максимум функции Ym = Ym(ω) и приравнять первую производную нулю; тогда, если

ωрезрезонансная частота, при которой амплитуда максимальна,радиан/сек
ω0частота собственных незатухающих колебаний системы,радиан/сек
mмасса колебательной системы,кг
βкоэффициентом вязкого трения,кг/сек
δкоэффициентом затухания,радиан/сек

Частота резонанса

\[ ω_{рез} = \sqrt{ω_{0}^2 - \frac{β^2}{2m^2}} = \sqrt{ω_{0}^2 - 2δ^2} \]

Резонансная частота ωрез несколько меньше частоты ω собственных колебаний системы с затуханием.

Условие отсутствия резонанса

\[ δ \geqslant \frac{ω_{0}}{\sqrt{2}} \]

При условии (2) явление резонанса совершенно исчезает. В этом случае при любой частоте возмущающей силы амплитуда колебаний меньше статического отклонения.

Амплитуда резонанса

Чтобы найти величину амплитуды в резонансном случае, нужно подставить формулу (1) в формулу отклонения при вынужденных колебаниях.

Если

Ymax.резрезонансная амплитуда колебаний системы,метр
Fmax.возммаксимальное значение возмущающей силы,Ньютон
mмасса колебательной системы,кг
ωрезрезонансная частота, при которой амплитуда максимальна,радиан/сек
ω0частота собственных незатухающих колебаний системы,радиан/сек
ωчастота колебаний системы с затуханием,радиан/сек
βкоэффициентом вязкого трения,кг/сек
δкоэффициентом затухания,радиан/сек

то имеем

\[ Y_m = \frac { F_{max.возм} } { β \sqrt{ ω_{0}^2 - \frac{β^2}{4m^2} } } \]
\[ Y_m = \frac{F_{max.возм}}{βω} \]
\[ Y_m = \frac{F_{max.возм}}{2δmω} \]

Согласно формуле, разность фаз α также зависит от частоты возмущающей силы. Параметром служит коэффициент δ.

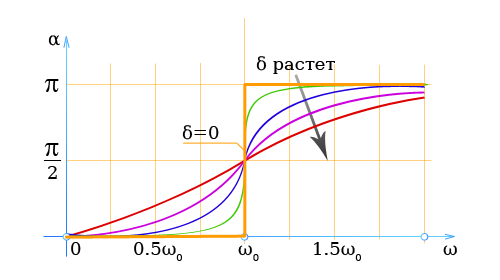
Резонанс
На рисунке представлена зависимость α от частоты.

Независимо от величины затухания при ω = ω0 разность фаз составляет

\[ α = 90° \]

Резонанс играет большую роль в технике и в повседневной жизни. В большинстве механических устройств под действием внешних периодических сил могут возникать колебания. При резонансе происходит нарастание амплитуды колебаний, и это может привести к разрушениям («резонансная катастрофа»). В случае вращательного движения резонансную частоту называют критическим числом оборотов.

Чтобы предотвратить возникновение колебаний со слишком большой амплитудой следует:
- по возможности устранять периодически действующие силы,
- добиваться большой разности собственной частоты и частоты возбуждающей силы,
- добиваться того, чтобы частота принимала резонансное значение лишь на время, меньшее одного периода колебаний,
- применять демпфирующие элементы.

Назад Вперед

Copyright © FXYZ.ru, 2007 — 2024.
Мобильная β версия | полная