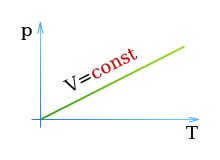
Изменение давления при нагревании, второй закон Гей-Люссака

Если

p_t	давление газа при произвольной температуре t,	Па
p₀	давление газа при температуре 0°С,	Па
t	температура,	0°С
β	термический коэффициент давления (коэффициент объемного расширения газа),	1/K

то

\[ p_t = p_0 ( 1 + βt ) \]

Из формулы (1) следует, что при температуре t₁

\[ p_1 = p_0 ( 1 + βt_1 ) \]

\[ p_1 = p_0 \bigg( 1 + \frac{t_1}{273.15} \bigg) \]

\[ p_1 = p_0 \bigg( 1 + \frac{t_1}{T_0} \bigg) \]

\[ p_1 = p_0 \bigg( \frac{T_0 + t_1}{T_0} \bigg) \]

а при другой температуре t₂ соответственно

\[ p_2 = p_0 ( 1 + β t_2 ) \]

\[ p_2 = p_0 \bigg( 1 + \frac{t_2}{273.15} \bigg) \]

\[ p_2 = p_0 \bigg( 1 + \frac{t_2}{T_0} \bigg) \]

\[ p_2 = p_0 \bigg( \frac{T_0 + t_2}{T_0} \bigg) \]

Разделив первое равенство на второе, получим

\[ \frac{p_1}{p_2} = \frac{T_0 + t_1}{T_0 + t_2} \]

или

\[ \frac{p_1}{p_2} = \frac{T_1}{T_2} \]

или

\[ \frac{p}{T} = \const \]

Второй закон Гей-Люссака

Второй закон Гей-Люссака гласит: Давление газа p в замкнутом объеме пропорционально абсолютной температуре газа T

\[ p \sim T \qquad (\enspace V = \const \enspace) \]

Формула (11) точно выполняется для идеальных газов, для реальных газов она является хорошим приближением и неприменима в случае пара.