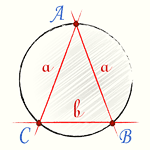
Радиус описанной окружности равнобедренного треугольника, формула

Радиус описанной окружности равнобедренного треугольника вычисляется по классической формуле

\[ R = \frac{a^2 b}{4\sqrt{p(p-a)(p-a)(p-b)}} \]

где

\[ p=\frac{1}{2}(a+a+b) \]

(a,b - стороны равнобедренного треугольника; R - радиус описанной окружности равнобедренного треугольника) После подстановок, преобразований и упрощений получается следующая формула:

\[ R = \frac{a^2}{\sqrt{(2a)^2-b^2}} \]

Вычислить, найти радиус описанной окружности равнобедренного треугольника по формуле (3)

Назад Вперед