Окружность в полярных координатах
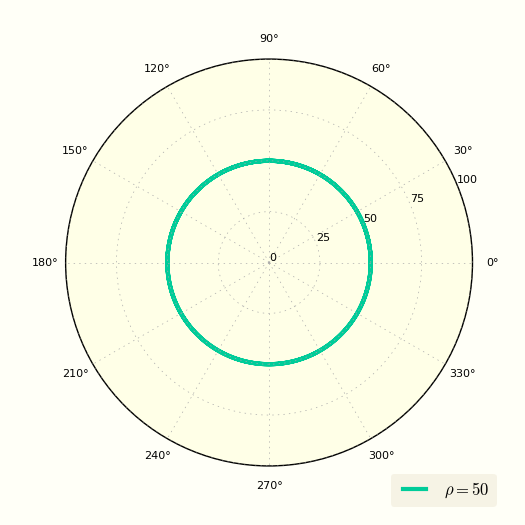
Уравнение окружности в полярных координатах выглядит очень просто
ρ=R=const(1)
Это уравнение показывает, что ρ вообще не зависит от угла φ.
Построение окружности по простому уравнению в полярной системе координат
Еще одно уравнение окружности в полярных координатах
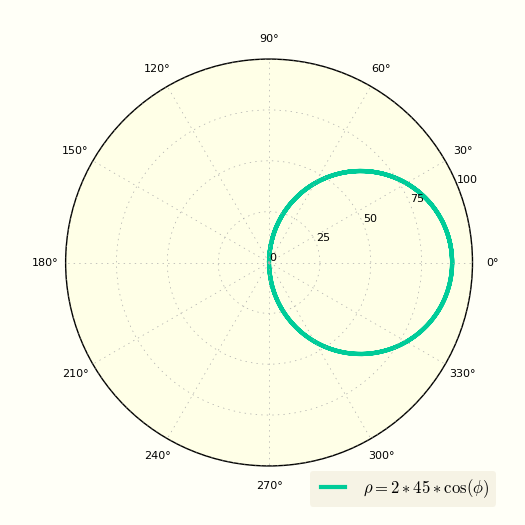
Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.
Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:
(x−R)2+y2=R2(2)
Также известны
формулы перевода декартовых координат в полярные
Используя эти формулы и подставив их в (1) мы получим:
Уравнение окружности в полярных координатах
Изначально после подстановки имеем
ρ2−2Rρcos(φ)=0(3)
И этого уравнения получается система
{ρ=0ρ=2Rcos(φ)(4)
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
ρ=2Rcos(φ)(5)
Построение окружности в полярной системе координат
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
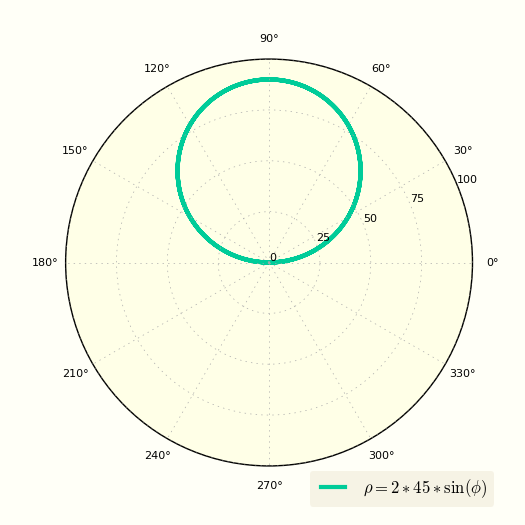
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.
При таком смещении окружность описывается уравнением:
x2+(y−R)2=R2(6)
Снова используем
формулы перевода декартовых координат в полярные
получаем:
ρ2−2Rρsin(φ)=0(7)
И этого уравнения получается система
{ρ=0ρ=2Rsin(φ)(8)
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
ρ=2Rsin(φ)(9)
Построение окружности в полярной системе координат смещенной вверх относительно полюса
Copyright © FXYZ.ru, 2007 — 2024.
Мобильная β версия | полная
