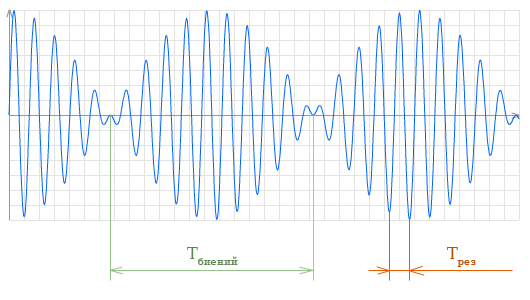
Частота биений

Период биений Т_б — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π.

Частота биений, Период биений, Результирующая частота

Поскольку при аргументе, равном π/2, 3π/2 …, косинус обращается в нуль, имеем:

\tag{1} \frac{ω_{{\htmlStyle{color: ForestGreen;}{1}}}-ω_{{\htmlStyle{color: ForestGreen;}{2}}}}{{\htmlStyle{color: ForestGreen;}{2}}} T_{б} = π

\tag{2} ω = {\htmlStyle{color: ForestGreen;}{2}}πf

\tag{3} \frac{{\htmlStyle{color: ForestGreen;}{2}}πf_{{\htmlStyle{color: ForestGreen;}{1}}}{\htmlStyle{color: ForestGreen;}{-2}}πf_{{\htmlStyle{color: ForestGreen;}{2}}}}{{\htmlStyle{color: ForestGreen;}{2}}} = π f_{б}

Решая это уравнение относительно частоты биений, получаем

\tag{4} f_{б} = f_{{\htmlStyle{color: ForestGreen;}{1}}} - f_{{\htmlStyle{color: ForestGreen;}{2}}}

Частота биений

Частота биений есть отношение числа минимумов амплитуды ко времени. Частота биений определяется как разность частот составляющих колебаний.

\tag{5} Т_{б} = \frac{ {\htmlStyle{color: ForestGreen;}{1}} }{ f_{б}}

\tag{6} Т_{б} = \frac{ T_{\htmlStyle{color: ForestGreen;}{1}} T_{\htmlStyle{color: ForestGreen;}{2}} }{ T_{\htmlStyle{color: ForestGreen;}{2}} - T_{\htmlStyle{color: ForestGreen;}{1}} }

\tag{7} f_{рез} = \frac{ f_{\htmlStyle{color: ForestGreen;}{1}} + f_{\htmlStyle{color: ForestGreen;}{2}} }{ {\htmlStyle{color: ForestGreen;}{2}} } = \overline{f}

Отсюда находим период результирующих колебаний Т_рез = 1/f_рез

\tag{8} Т_{рез} = {\htmlStyle{color: ForestGreen;}{2}} \frac{ T_{\htmlStyle{color: ForestGreen;}{1}} T_{\htmlStyle{color: ForestGreen;}{2}} }{ T_{\htmlStyle{color: ForestGreen;}{1}} + T_{\htmlStyle{color: ForestGreen;}{2}} }

Вычислить, найти частоту биенй по формуле (4)

f₁ (частота, Гц)	×10 в степени
f₂ (частота, Гц)	×10 в степени

Частота биений, формула